Maximum Value Contiguous Subsequence Dynamic Programming

Maximum Subsequence Sum Problem (MCSS)

Before we get started let me remind you that this is a series of short articles on Dynamic Programming. You can refer to the first article (introduction) here. In this article we are going to discuss a new problem (MCSS) that can be solved efficiently using Dynamic Programming. The MCSS problem is an easy example on DP but it can be solved in different ways. In this article DP approach is discussed however if you are interested in other ways to solve it you can refer to this post.

Problem Definition

Given an array of (n) integers. The array is expected to have positive as well as negative integer numbers. We are asked to find the contiguous subsequence of maximal sum of the array. In other words we need to find a contiguous range of integers in the array that has the largest sum.

Solution

The maximum contiguous subsequence problem is going to be trivial if the array contains only positive integers because we can just take the sum of the whole array as our solution. If the the array contains a mix of positive and negative integers then it becomes more interesting. Take a look at the following example:

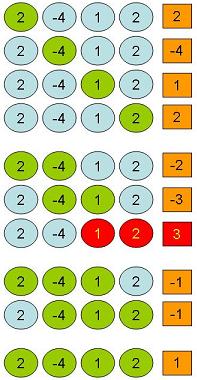
Note that the first group of contiguous sub sequences have a length of (1), The second group have a length of (2) then (3) then (4). We just enumerated all possible contiguous sub sequences then computed the sum of each. It turned out that the MCSS is the sub sequence consisting from the third and fourth elements in the original array {1, 2} and the maximum sum is (3). Brute force solution applies a similar approach by figuring out all possible sub sequences we might have then finding the one with largest sum. Dynamic Programming on the other hand has a better running time. We can solve this problem in linear time as opposed to (n^2) in case of brute force (as it requires two nested loops) so let us apply the techniques we have already learned so far.

Characterize the structure of an optimal solution

Ask the typical question: What are we intending to optimize. The answer is maximizing the sum of contiguous elements in the input array (not all elements but some sub sequence). We need to recursively express the sum of an arbitrary contiguous sub sequence in the original array in terms of smaller size instances of the same problem. In other words we need to express that sum in terms of already computed values.

Recursively define the value of an optimal solution

Let the maximum sum of all sub sequences ending at position (j) in the input array be M[j] for example:

The general formula can be easily deduced as follows:

In plain English this means the maximum sum of all possible windows (sub sequences) ending at position (j) can be attained if we either extend the window ending at position (j-1) or start a new window at position (j). Let us apply this recursive formula to the example array we mentioned earlier:

So the MCSS is (3) and the sub sequence with maximum sum ends at (j = 4). As you can see we were able to compute the MCSS value and determine where it ends but we have not determined yet where does it start. This concept repeats in every DP problem where computing the optimal value is one part of the solution but outlining the steps to get the optimal solution is another part. Computing the optimal value is done in a bottom up fashion (we will do that in the next section) by filling the array M[j] where (j) goes from (1) to (n) then taking the largest value in the array M[j] as our optimal value (MCSS). The second part of the solution is determining where the sub sequence with maximum sum starts. This can be solved using back pointers. Let us use another (one dimensional) array called (b) to store the array position at which the window (sub sequence) ending at position (j) with maximum sum starts. Recall that M[j] = max (A[j], A[j] + M[j-1]) so set b[j] = j when a new window starts and set b[j] = b[j-1] when the current window is extended.

Compute the value of an optimal solution in a bottom up fashion

In the previous section we explained what arrays (M and b) need to be populated and why. The pseudo code below demonstrates that:

Construct an optimal solution from the computed information

The solution was already constructed in the previous step due to the simplicity of the problem. Filling the array (M), finding the largest element in (M) and using back pointers array (b) to mark the start of the sub sequence of maximum sum all done in one step which was demonstrated in the previous block of pseudo code.

We are done with part 5. In the next part I will explain the 5th Dynamic Programming problem “Longest Increasing Sub Sequence“. Please use the comments section below for questions, corrections or feedback. Thanks for reading.