November 29, 2011

Dynamic Programming Longest Increasing Sub Sequence

Longest Increasing Sub Sequence

Welcome to the 6th part of our discussion on Dynamic Programming. You can refer to the first article (introduction) here. In this article we are going to discuss the “Longest Increasing Sub Sequence” problem which can be solved efficiently using Dynamic Programming.

Problem Definition

Given a sequence of numbers [A1 .. An] we need to find a longest strictly increasing sub sequence not necessarily contiguous. For example if the input sequence is [9, 11, 2, 13, 7, 15] then the sequence [9, 11, 13, 15] is the longest strictly increasing sub sequence. Each number in the sub sequence is greater than the previous number and not necessarily contiguous.

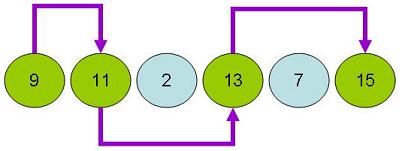
Solution

Let us return back to our example sequence [9, 11, 2, 13, 7, 15]. Here are sample strictly increasing sub sequences:

Sub sequences of length = 2
[9, 11] 
[2, 13] 
[2, 7] 
[7, 15]

Sub sequences of length = 3
[9, 11, 13] 
[2, 7, 15]

Sub sequences of length = 4
[9, 11, 13, 15]

Sub sequences of length = 2

[9, 11]

[2, 13]

[2, 7]

[7, 15]

Sub sequences of length = 3

[9, 11, 13]

[2, 7, 15]

Sub sequences of length = 4

[9, 11, 13, 15]

Now notice the following:

The longest increasing sub sequence ending at position (1) is [9]
The longest increasing sub sequence ending at position (2) is [9, 11]
The longest increasing sub sequence ending at position (3) is [2]
The longest increasing sub sequence ending at position (4) is [9, 11, 13]
The longest increasing sub sequence ending at position (5) is [2, 7]
The longest increasing sub sequence ending at position (6) is [9, 11, 13, 15]

Now let us define L(j) to be the length of the longest increasing sub sequence ending at position (j):

L(1) = Length ([9]) = 1
L(2) = Length ([9, 11]) = 2
L(3) = Length ([2]) = 1
L(4) = Length ([9, 11, 13]) = 3
L(5) = Length ([2, 7]) = 2
L(6) = Length ([9, 11, 13, 15]) = 4

L(1) = Length ([9]) = 1

L(2) = Length ([9, 11]) = 2

L(3) = Length ([2]) = 1

L(4) = Length ([9, 11, 13]) = 3

L(5) = Length ([2, 7]) = 2

L(6) = Length ([9, 11, 13, 15]) = 4

Note that the general form is:

L(j) = 1 + MAX ( L(i) ) where i < j and A[i] < A[j]

1	L(j) = 1 + MAX ( L(i) ) where i < j and A[i] < A[j]

Let us apply the formula and see that it really works:

//Nothing because there are no elements before j = 1
L(1) = 1 + MAX (nothing) = 1
L(2) = 1 + MAX (L(1)) = 1 + 1 = 2

//Nothing because there are no elements A[i] 
//before j = 3 that satisfy A[i] < A[3]
L(3) = 1 + MAX (nothing) = 1
L(4) = 1 + MAX (L(3), L(2), L(1)) = 1 + MAX (1, 2, 1) = 1 + 2 = 3

//We did not say MAX (L(4), L(3), L(2), L(1)) 
//because A[4], A[2], A[1] all do not satisfy A[i] < A[5]
L(5) = 1 + MAX (L(3)) = 1 + 1 = 2
L(6) = 1 + MAX (L(5), L(4), L(3), L(2), L(1)) 
     = 1 + MAX (2, 3, 1, 2, 1) 
     = 1 + 3 = 4

//Nothing because there are no elements before j = 1

L(1) = 1 + MAX (nothing) = 1

L(2) = 1 + MAX (L(1)) = 1 + 1 = 2

//Nothing because there are no elements A[i]

//before j = 3 that satisfy A[i] < A[3]

L(3) = 1 + MAX (nothing) = 1

L(4) = 1 + MAX (L(3), L(2), L(1)) = 1 + MAX (1, 2, 1) = 1 + 2 = 3

//We did not say MAX (L(4), L(3), L(2), L(1))

//because A[4], A[2], A[1] all do not satisfy A[i] < A[5]

L(5) = 1 + MAX (L(3)) = 1 + 1 = 2

L(6) = 1 + MAX (L(5), L(4), L(3), L(2), L(1))

= 1 + MAX (2, 3, 1, 2, 1)

= 1 + 3 = 4

In plain English a sub sequence strictly increasing of maximum length ending at position (j) must be an extension to another sub sequence strictly increasing of maximum length ending at a previous position (i) where A[i] is less than A[j]. Note that the condition i < j and A[i] < A[j] means we might have more than one sub sequences satisfying this condition. In other words the element A[j] at position (j) can be an extension to more than one strictly increasing sub sequence but we take the sub sequence of maximum length that is why we we have MAX(L(i)) in the formula. Once the array L(j) is fully populated we must scan the whole array to find the (j) value with largest L(j). At each position (j) there is a maximum length strictly increasing sub sequence ending there but we are concerned about the one with maximum length across the whole input array. Printing out the individual elements that form the increasing sub sequence can be done using back pointers. We need to have a back pointers array b[j] to save the (i) value that satisfies the condition mention earlier:

MAX (L(i)) where i < j and A[i] < A[j]

1	MAX (L(i)) where i < j and A[i] < A[j]

Once b[j] is filled we can scan the table to print the actual numbers in the increasing sub sequence. We will demonstrate that in the last section of this article. We are ready now to proceed with our Dynamic Programming solution. Characterize the structure of an optimal solution

The value we are trying to optimize is a length value. We are intending to maximize the length of a strictly increasing sub sequence in the original input array. We already saw that a sub sequence of maximum length ending at some position (j) is an extension to another sub sequence strictly increasing ending at an earlier position (i). Since there might be more than one strictly increasing sub sequence depending on the value of (i) we take the longest one. Let us define that recursively in the following section.

Recursively define the value of an optimal solution

Let L(j) be the length of a strictly increasing sub sequence ending at position (j). We have shown that L(j) can be expressed as:

L(j) = 1 + MAX (L(i)) where i < j and A[i] < A[j]

1	L(j) = 1 + MAX (L(i)) where i < j and A[i] < A[j]

Note that the values L(i) for each (i) less than (j) overlap. These sub problems use each other for example L(3) is used in L(6), L(5) and L(4) as demonstrated before (You can go back to refresh your memory if you forgot). I will keep repeating this concept as it is very important to put in mind. In Dynamic Programming new values are computed while already computed values are only looked up in a table. In the next section we will build our tables in a bottom up fashion.

Compute the value of an optimal solution in a bottom up fashion

We already explained the Dynamic Programming solution in general. Below you can find the actual algorithm to populate L(j) and b(j) in pseudo code. Code is explained in details using comments. Take a look:

//This variable saves the length of the longest 
//increasing sub sequence satisfying the condition
//i < j and A[i] < A[j] if you forgot that go back 
//and refresh your memory
int maxi = 0;

//This variable saves the length of the longest 
//increasing sub sequence across all (j) values.
//Recall that we said once L[j] is populated we
//need to find the largest value in L[j]
int maxj = 1;

//This variable points to the (j) value at which 
//the longest increasing sub sequences ends. 
//It is going to be the start point to print the
//individual elements in the solution using back
//pointers array b[j]
int end = 1;

//The length of the strictly increasing sub sequence 
//ending at position (1) is also (1) because it only 
//contains one number which is A[1]
L[1] = 1;

//We already initialized L(1) so we compute the 
//rest of L(j) values as (j) goes from (2) to (n)
for (j = 2; j <= n; j++)
{
	//Recall that b[j] points to the array 
	//element in (A) from which the current 
	//sub sequence was extended so we initially 
	//set b[j] = j in case the current sequence 
	//was not extended (started new sequence) 
	//then we update that later in case it was 
	//indeed extended
	b[j] = j;

	//For all i < j find the longest strictly 
	//increasing sub sequence from which the 
	//current sequence ending at (j) was extended 
	for (i = 1; i < j; i++)
	{
		//Pay attention here. We have two conditions.
		//The first condition A[i] < A[j] is used to 
		//make sure the sequence ending at (j) is indeed 
		//strictly increasing by extending a previous sub 
		//sequence ending at some position (i). The second 
		//condition L(i) > maxi is used to find the longest
		//strictly increasing sub sequence from which to
		//extend the current sequence at (j). Again I repeat
		//if you lost track go back to the explanation 
		//mentioned earlier in the article.
		if (A[i] < A[j] && L[i] > maxi) 
		{
			//Update maxi whenever a longer 
			//sub sequence is found
			maxi = L[i];

			//Save the (i) value at which the 
			//longest sub sequence was found
			//This (i) value is a back pointer
			//needed to construct the actual solution
			b[j] = i;
		}
	}

	//Refer back to the explanation at the 
	//beginning of the article. We showed that
	//L(j) = 1 + Max (L(i)) where i < j and A[i] < A[j] L[j] = 1 + maxi; 
	//Reset the variable maxi for the next (j) value maxi = 0; 
	//Recall that we said earlier just 
	//populating L(j) is not the solution however 
	//we need to find the largest value in L(j) 
	if (L[j] >= maxj)
	{
		//Keep updating until we get the largest value
		maxj = L[j];

		//Save the (j) value at which the longest 
		//increasing sub sequence (The solution we 
		//are looking for) ends. This value is used 
		//as the start point to generate the actual 
		//solution using back pointers.
		end = j;
	}
}

//This variable saves the length of the longest

//increasing sub sequence satisfying the condition

//i < j and A[i] < A[j] if you forgot that go back

//and refresh your memory

int maxi = 0;

//This variable saves the length of the longest

//increasing sub sequence across all (j) values.

//Recall that we said once L[j] is populated we

//need to find the largest value in L[j]

int maxj = 1;

//This variable points to the (j) value at which

//the longest increasing sub sequences ends.

//It is going to be the start point to print the

//individual elements in the solution using back

//pointers array b[j]

int end = 1;

//The length of the strictly increasing sub sequence

//ending at position (1) is also (1) because it only

//contains one number which is A[1]

L[1] = 1;

//We already initialized L(1) so we compute the

//rest of L(j) values as (j) goes from (2) to (n)

for (j = 2; j <= n; j++)

{

//Recall that b[j] points to the array

//element in (A) from which the current

//sub sequence was extended so we initially

//set b[j] = j in case the current sequence

//was not extended (started new sequence)

//then we update that later in case it was

//indeed extended

b[j] = j;

//For all i < j find the longest strictly

//increasing sub sequence from which the

//current sequence ending at (j) was extended

for (i = 1; i < j; i++)

{

//Pay attention here. We have two conditions.

//The first condition A[i] < A[j] is used to

//make sure the sequence ending at (j) is indeed

//strictly increasing by extending a previous sub

//sequence ending at some position (i). The second

//condition L(i) > maxi is used to find the longest

//strictly increasing sub sequence from which to

//extend the current sequence at (j). Again I repeat

//if you lost track go back to the explanation

//mentioned earlier in the article.

if (A[i] < A[j] && L[i] > maxi)

{

//Update maxi whenever a longer

//sub sequence is found

maxi = L[i];

//Save the (i) value at which the

//longest sub sequence was found

//This (i) value is a back pointer

//needed to construct the actual solution

b[j] = i;

}

//Refer back to the explanation at the

//beginning of the article. We showed that

//L(j) = 1 + Max (L(i)) where i < j and A[i] < A[j] L[j] = 1 + maxi;

//Reset the variable maxi for the next (j) value maxi = 0;

//Recall that we said earlier just

//populating L(j) is not the solution however

//we need to find the largest value in L(j)

if (L[j] >= maxj)

{

//Keep updating until we get the largest value

maxj = L[j];

//Save the (j) value at which the longest

//increasing sub sequence (The solution we

//are looking for) ends. This value is used

//as the start point to generate the actual

//solution using back pointers.

end = j;

}

Construct an optimal solution from the computed information

The final step is to print out the individual elements that construct the solution. We achieve this using back pointers array b[j]. Note that the pseudo code below does that in reverse order. You can modify it on your own if you wish to print the elements in order.

print ("Maximum increasing sub sequence length = ", maxj);
print ("Elements of the maximum increasing sub sequence:");

//Start at the (j) position (end variable) at 
//which the (grand) longest strictly increasing 
//sub sequence ends then trace back using the 
//array b[j]. Recall that for each value (j) 
//there is a b[j] value that points to the 
//previous sub sequence from which the 
//current sequence was extended
for (int j = end; j > 1; j = b[j])
{
        print A[j];
}

//The last element in the solution is 
//printed alone to prevent the previous 
//loop from going infinite.
print A[b[1]];

print ("Maximum increasing sub sequence length = ", maxj);

print ("Elements of the maximum increasing sub sequence:");

//Start at the (j) position (end variable) at

//which the (grand) longest strictly increasing

//sub sequence ends then trace back using the

//array b[j]. Recall that for each value (j)

//there is a b[j] value that points to the

//previous sub sequence from which the

//current sequence was extended

for (int j = end; j > 1; j = b[j])

{

print A[j];

}

//The last element in the solution is

//printed alone to prevent the previous

//loop from going infinite.

print A[b[1]];

We are done with part 6. In the next part I will explain the 6th Dynamic Programming problem “Making Change“. Please use the comments section below for questions, corrections or feedback. Thanks for reading.

8 BIT AVENUE

Dynamic Programming Longest Increasing Sub Sequence

More from my site

About Author

Mohammed Abualrob

Add a Comment