Dynamic Programming Longest Common Subsequence
Longest Common Subsequence
Welcome to the 4th article on Dynamic Programming. You can refer to the first article (introduction) here. I will be using the shortcut LCS to refer to longest common sub-sequence. Let us get started.
Introduction
One of the applications of “Longest Common Subsequence” problem is comparing DNA strings to see how similar they are. Given two DNA strings we need to find a third string in which the bases (symbols) appear in both original strings in the same order but not necessarily consecutively. The following schematic diagram shows two strings and the longest common sub sequence string.
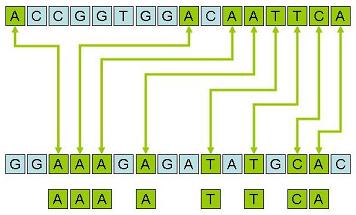
Problem definition
- Given the first sequence which contains (m) symbols X = (x1, x2, x3, …, xm)
- Given the second sequence which contains (n) symbols Y = (y1, y2, y3, …, yn)
- Find the longest common sequence (Z) between (X) and (Y) call it Z = (z1, z2, z3, …, zk)
Solution
One can think of a brute force solution to this problem but it is not going to be an efficient solution. For example there are (2^m) possible sub sequences in (X) so trying all possible sub sequences in both strings then taking the longest common sequence is not going to be a good approach.
Dynamic Programming on the other hand can be used to find an efficient solution for the LCS problem. Let us first agree on some notation before we proceed in the solution.
- (xi) means symbol at position (i) in the sequence (X) for example (x1) is the first symbol in (X) and (xm) is the last symbol in (X) assuming (X) contains (m) symbols.
- (Xi) means the sub sequence (in X) of all symbols starting at (x1) ending at (xi).
- Points (1) and (2) above apply also to the second sequence (Y) and the LCS sequence (Z).
Now consider the following cases:
- if (xm == yn) then (zk = xm = yn) and Z(k-1) is an LCS of X(m-1) and Y(n-1). This means if the last symbol in both sequences is the same then it (last symbol) is going to be the last symbol in the common sequence between the two sequences. It also means the string resulting from removing this symbol from the LCS is also another LCS for both strings after removing the last symbol from each one of them.
- if (xm != yn) and (zk != xm) implies (Z) is an LCS of X(m-1) and (Y). This means if the last symbol (xm) in (X) is different from the last symbol (yn) in (Y) and at the same time it (xm) is different from the last symbol (zk) in the LCS then this implies that the LCS (Z) is common to (Y) and (X) removing the last symbol (xm) from (X).
- Similarly if (xm != yn) and (zk != yn) implies (Z) is an LCS of (X) and Y(n-1). This means if the last symbol (yn) in (Y) is different from the last symbol (xm) in (X) and at the same time it (yn) is different from the last symbol (zk) in the LCS then this implies that the LCS (Z) is common to (X) and (Y) removing the last symbol (yn) from (Y).
Here is an example on case 1:
|
1 2 3 |
X = A B C D // m = 4 Y = B A B D // n = 4 Z = A B D // k = 3 |
Note that x4 = y4 = z3 = D (xm = yn = zk) so Z(k-1) is an LCS of X(m-1) and Y(n-1). In other words (Z2) is an LCS of (X3) and (Y3) as shown below:
|
1 2 3 |
X = A B C Y = B A B Z = A B |
Here is an example on case 2 (Case 3 is very similar to case 2):
|
1 2 3 |
X = A B C D // m = 4 Y = B A B B // n = 4 Z = A B // k = 2 |
Note that x4 != y4 and z2 != x4 so (Z) is an LCS of X(m-1) and Y. In other words (Z) is an LCS of (X3) and (Y) as shown below:
|
1 2 3 |
X = A B C Y = B A B B Z = A B |
Characterize the structure of an optimal solution
Let us ask the typical question “what are we intending to optimize”. The answer to this question is finding the maximum length sequence common to the two input strings. The three cases outlined above characterize the structure of an optimal solution. Proceed to the next section for a recursive definition of such an optimal solution.
Recursively define the value of an optimal solution
Let C[i, j] be the length of the longest common sequence between the sub sequences (Xi) and (Yj). Please refer to the previous sections to refresh your memory if you forgot what (Xi) and (Yj) mean. We have three cases:
- If (i = 0) or (j = 0) then C[i, j] = 0. This means if the length of the sub sequence (Xi) or (Yj) is zero then the LCS between the two is zero as well.
- If (i > 0 and j > 0 and xi = yj) then C[i, j] = C[i-1, j-1] + 1. This means if the last symbol in both sub sequences (Xi) and (Yj) is equal then the LCS between the two is one (symbol) plus the LCS of the remaining (excluding last symbol) symbols in both sub sequences. We already explained that earlier. You can go back to refresh your memory.
- If (i > 0 and j > 0 and xi != yj) then C[i,j] is the max (C[i, j-1], C[i-1, j]). This means if the last symbol (xi and yj) of the sub sequences (Xi) and (Yj) is different then we have two cases. Case one is when the last symbol (zk) in the sub LCS (Zk) is different from (xi). Case two is when the last symbol (zk) in the sub LCS (Zk) is different from (yj). We just take the maximum of the two because we are looking for the longest common sub sequence. I recommend that you refresh your memory again and go back read the three cases discussed earlier.
Let us write the recursive formula for C[i, j] in one place:
|
1 2 3 |
C[i, j] = 0 if i = 0 or j = 0 C[i, j] = 1 + C[i-1, j-1] if i > 0 and j > 0 and xi = yj C[i, j] = max (C[i, j-1], C[i-1, j]) if i > 0 and j > 0 and xi != yj |
As you can see above the values C[i-1, j-1], C[i, j-1] and C[i-1, j] overlap. Whenever a new value is computed it is saved in the table C[i, j] (two dimensional array). Whenever an already computed values is referenced it is looked up in the table.
Compute the value of an optimal solution in a bottom up fashion
Filling the table C[i, j] for all values of (i) and (j) should be straightforward. (i) goes from (1) to (m) and (j) goes from (1) to (n). We start with special cases when (i = 0 or j = 0) then all other values use each other in the computation. That is the nature of Dynamic Programming only new values are computed from the scratch while already computed values are only looked up. By just filling the table C[i, j] then computing the value C[m, n] we can compute the length of the longest common sub sequence (Z) however that is only one part of the solution. We need to know exactly how to construct the sequence and print out the individual symbols in (Z). In order to do that we need a back pointers array so that we can track which symbols are included in the solution. Let us call this array b[i, j]. For each value b[i, j] we store a mark (1 or 2 or 3) to indicate one of three scenarios (The ones discussed earlier in this article):
|
1 2 3 |
1.0 Set b[i, j] = 1 if (xi == yj) 2.a Set b[i, j] = 2 if (xi != yj) and C[i-1, j] >= C[i, j-1] 2.b Set b[i, j] = 3 if (xi != yj) and C[i-1, j] < C[i, j-1] |
If you forgot these cases I recommend again (and again) to go back and read the three cases we explained earlier. In summary they check the last symbol (xi and yj) in each sub sequence (Xi and Yj). If they are equal then the symbol (xi = yj) is included in the LCS (Zk) of the two sub sequences. If that is the case we mark b[i, j] = 1. If they (xi and yj) are not equal then we have two cases. The first case (2.a) is when the last symbol (zk) in the LCS (Zk) of the two sub sequences (Xi and Yj) is different from the last symbol (xi) in the first sub sequence (Xi). In this case we set b[i, j] = 2 if it is greater than that in the second case (2.b). The second case (2.b) is when the last symbol (zk) in the LCS (Zk) of the two sub sequences is different from the last symbol (yj) in the second sub sequence (Yj). In this case we set b[i, j] = 3 if it is greater than that in the first case (2.a). I know it is confusing and specially if you get lost with acronyms and symbol names. It is a good idea to try applying these rules on short strings like the example (m = 4, n = 4, k = 3) provided earlier in this article. Now we are ready to write the pseudo code to fill the look up and back pointers tables. Here it is:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
//Whenever j = 0 set C[i, j] = 0 for (int i = 1; i <= m; i++) { C[i, 0] = 0; } //Whenever i = 0 set C[i, j] = 0 for (int j = 1; j <= n; j++) { C[0, j] = 0; } //First strings has (m) symbols for (int i = 1; i <= m; i++) { //Second string has (n) symbols for (int j = 1; j <= n; j++) { //Case 1 when they are equal if (xi == yj) { C[i, j] = 1 + C[i-1, j-1]; b[i, j] = 1; } //Case 2.a else if (C[i-1, j] >= C[i, j-1] { C[i, j] = C[i-1, j]; b[i, j] = 2; } //Case 2.b else { C[i, j] = C[i, j-1]; b[i, j] = 3; } } } |
The code above obviously runs in polynomial time. We have two nested loops so the running time is O[m*n]. Once the tables are completely filled then we can just take C[m, n] to compute the length of the longest common sub sequence however we are not done yet. We need to print out the individual symbols of the longest common sub sequence. This is taken care of in the next section.
Construct an optimal solution from the computed information
Here is a recursive function that prints the individual bases or symbols of the LCS. It takes the following input parameters:
- Back pointers array (b)
- The first sequence (X). Note that there is no need to pass the second sequence (Y). Only one of them is needed because we are printing the common symbols.
- Index parameters (i) and (j) because we stored a mark or a back pointer in (b) for each [i, j] combination
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
PrintLCS(b, X, i, j) { //Remember that C[i, j] = 0 when i or j = 0 so //in this case nothing is done if (i == 0 || j == 0) return; //Case 1 when xi = yj so we print (xi) which is //going to be a symbol in the LCS then we call the //recursive function on the sub sequences X(i-1) //and Y(j-1) if (b[i,j] == 1) { PrintLCS(b, X, i-1, j-1); print xi; } //Case 2 when xi != yj and (Zk) is //the LCS of the sub sequences X(i-1) //and Yj else if (b[i, j] == 2) { PrintLCS(b, X, i-1, j); } //Case 3 when xi != yj and (Zk) is //the LCS of the sub sequences Xi //and Y(j-1) else { PrintLCS(b, X, i, j-1); } } |
Take a look at the function above and notice the following:
- The function should be initially called with parameters (i = m, j = n) because our Dynamic Programming approach inspects the last two symbols in each sub sequence then goes back.
- The function prints the symbols in the LCS (Z) in reverse order. That is due to the same reason as we are inspecting symbols starting at the end of the string. If you are interested you can fix this on your own.
- Running time of this function should be in polynomial time as opposed to exponential time. It is not always easy to get a closed form of the running time for recursive functions but if you are interested you can research it on your own. It should not be worse than O(m*n).
We are done with part 4. In the next part I will explain the 4th Dynamic Programming problem “Maximum Contiguous Sub Sequence Sum“.
Please use the comments section below for questions, corrections or feedback. Thanks for reading.


The link to introduction at the start is pointing to the wrong url https://www.8bitavenue.com/2011/11/intorduction-to-dynamic-programming/. Please note the typo “intorduction”. Please fix it.
Your articles are Amazing. I can’t thank you enough for the super clear explanation of concepts.
thank you very much
The link to introduction at the start is pointing to the wrong url https://www.8bitavenue.com/2011/11/intorduction-to-dynamic-programming/. Please note the typo “intorduction”. Please fix it.
Your articles are Amazing. I can’t thank you enough for the super clear explanation of concepts.
thank you very much
“…The following schematic diagram shows two strings and the longest common sub sequence string.”
The answer should be “GGGGAATCA”. Please check again!