December 15, 2011
HomeAlgorithms and Data StructuresDynamic Programming Moving on a Checkerboard

Dynamic Programming Moving on a Checkerboard

By  Algorithms and Data Structures, Articles and Tutorials  3 Comments

Moving on a Checkerboard

Welcome to a new article on Dynamic Programming. Today we will discuss “Moving on a Checkerboard” problem. This is part 9 of a series of articles on the topic. You can refer to the first article here. Let us get started.

Problem Definition

We are given a grid of squares or a checkerboard with (n) rows and (n) columns. There is a profit we can get by moving to some square in the checkerboard. Our goal is to find the most profitable way from some square in the first row to some square in the last row. We can always move to the next square on the next row using one of three ways:

  1. Go to the square on the next row on the previous column (UP then LEFT)
  2. Go to the square on the next row on the same column (UP)
  3. Go to the square on the next row on the next column (UP then RIGHT)

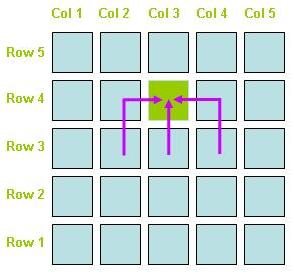
Once we are able to determine the most profitable way from any square in the first row to any square in the last row we can select the best way out of all these ways. Here is a schematic diagram to get a better idea bout this problem:

Characterize the structure of an optimal solution

The value we are trying to optimize is a profit value. We need to maximize the profit we get by moving to a particular square. Let us now try to figure out the structure of an optimal profit value. Suppose that you got the maximum profit value by moving to some square in the checker board. This maximum value is nothing but the sum of two values. The first one is the maximum profit value you get by moving to a previous square on the previous row (take a look at the schematic diagram above). The second one is the profit you get by moving from the previous square to the current square. Recall that there are three ways to move to a particular square from the previous row (up, up then right, up then left) so we need to select the one that yields maximum profit. Note that this structure of an optimal profit value is indeed a recursive structure. The optimal profit value to a particular square is defined in terms of optimal profit value to a previous square on the previous line. Note also that sub problems repeat for example in order to move to square [3, 3] you might move from squares {[2, 2] or [2, 3] or [2, 4]} on the previous row and in order to move to square [3, 4] you might move from squares {[2, 3] or [2, 4] or [2, 5]}. As you can see squares [2, 3] and [2, 4] are repeated. In Dynamic Programming we calculate values only once. If they are referenced again we just lookup these values from a table. In next section we will formally define the structure of an optimal solution using recursion.

Recursively define the value of an optimal solution

In this problem it is assumed that starting at any square at the first row does not yield any profit because we gain profit as we move to the next square. Please keep this in mind because it is going to be the initial case from which we will build the whole profit table in a bottom up fashion in the next step. There are two other special cases that we need to pay attention to. The first case when we are on a square on the first column. In this case we can only move up or up then right but we can not move up then left. The second case is similar but applies to the last column. In this case we can only go up or up then left. These two special cases will define the accepted range of row and column numbers as we define our recursive formula.

Let D[i, j] be the maximum profit that we can get by moving to a square at row number (i) and column number (j). This profit value (as we already pointed out earlier) is the addition of two values. The first one is the value we get by moving to square [i, j] from some square at the previous line. The second value is the maximum profit we already got by moving all the way from the first row until the previous line. The square at the previous line from which we moved to the current square at [i, j] can be one of the following:

  1. [i-1, j-1] means square at the previous line and previous column.
  2. [i-1, j] means square at the previous line and current column.
  3. [i-1, j+1] means square at the previous line and next column.

Since we have three different ways to move then we choose the one that yields maximum profit. We are ready now to define our recursive formula:

C++
1
2
3
4
5
6
7
8
9
10
11
12
D[1, j] = 0
D[i, j] = max
{
//Applies to squares not on the first column
D[i-1, j-1] + P(i-1, j-1) j > 1
 
//Applies to all squares
D[i-1, j] + P(i-1, j)
 
//Applies to squares not on the last column
D[i-1, j+1] + P(i-1, j+1) j < n
}

Note that P(m, k) means the profit we get when moving from square [m , k] to the current square [i, j]. Note that the condition (j > 1) means if square [i, j] is on the first column then we can move to it from the previous line either by going up or going up then left but we can not go up then right. Similarly if the square [i, j] is on the last column then we can move to it from the previous line either by going up or up then right but we can not go up then left. If the square [i, j] is in between then we have all the three ways to choose from.

Once the array D[i, j] is completely filled then we can find the most profitable way by taking the maximum over all D[n, j]. Note that D[n, j] means most profitable way to move from somewhere on the first row to some other square on the last row. The actual steps needed to take that path can be determined by using back pointers so let us define our back pointers array now.

Let w[i, j] store the column number (j) of the previous square from which we moved to the current square at [i,j]. Recall as we move from the bottom of the checkerboard to the top row we always increment the row number so that is easy to determine but the column number can change depending on which way we choose next that is why we need to save it so that we can print the path of the most profitable way starting at the first row ending at the last row. In the next section we will be filling the tables D[i, j] and w[i,j] in a bottom up fashion.

Compute the value of an optimal solution in a bottom up fashion

We explained what the tables (D) and (w) stand for. The following pseudo code demonstrates how to populate these tables in a bottom up fashion. Once the tables are populated, the actual solution can be constructed from back pointers. We will do this in the last step.

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
//Profit is zero when we start at the first row
//We earn profit as we move up the checkerboard
for (int j = 1; j <= n; j++)
{
D[1, j] = 0;
}
 
//For each row
for (int i = 2; i <= n; i++)
{
//For each column
for (int j = 1; j <= n; j++)
{
//Case 1: Moving from the previous line on the same column
//It applies to any square int max = D[i-1, j] + P(i-1, j);
//Save back pointer w[i, j] = j;
//Case 2: Moving from the previous line on the previous column
//It does not apply to squares on the first column
if (j > 1 && D[i-1, j-1] + P(i-1, j-1) > max)
{
//Update the max
max = D[i-1, j-1] + P(i-1, j-1);
 
//Save back pointer
w[i, j] = j-1;
}
 
//Case 3: Moving from the previous line on the next column
//It does not apply to squares on the last column
if (j < n && D[i-1, j+1] + P(i-1, j+1) > max)
{
//Update the max
max = D[i-1, j+1] + P(i-1, j+1);
 
//Save back pointer
w[i, j] = j+1;
}
 
//Select the largest profit value
D[i, j] = max;
}
}
 
//Recall that D[i, j] gives us the most profitable
//way to square [i, j] so we need to find the largest
//(D) value for all columns in the last row by finding
//the maximum over all (j) in D[n, j]
 
//Initialize the max (D) value and the (j) value
//that corresponds to the max profit
int maxd = D[1, 1];
int maxj = 1;
 
//For each column in the last row (n)
for (int j = 2; j <= n; j++) { if (D[1, j] > maxd)
{
//Update max
maxd = D[1, j]
//Save column number
maxj = j;
}
}
 
//Print the max profit
print ("Maximum profit is: ", maxd);
 
//Print the steps needed to make the max profit
//This is done in the last step when we construct
//the solution from back pointer array w[i, j]
PrintSquares(w, n, maxj);

Construct an optimal solution from the computed information

The last step is to construct the needed moves to achieve maximum profit. This can be done by tracing the back pointers array w[i, j] as in the following pseudo code:

C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//The function receives the back pointers array (w)
//as input. It also receives the row and column numbers.
//This function is called in the previous step starting
//at the last row (n) and the column number (maxj) that
//gave the largest profit (D)
PrintSquares(int w[], int i, int j)
{
//Base case. Stop printing when
//when (i = 0) because rows start at 1
if (i == 0)
{
return;
}
 
//Print square row and column numbers
print("Square at row ", i, " and column ", j);
 
//Recursively call the function. Row numbers
//are decremented each time because we are
//printing the squares backwards. Column numbers
//are saved in the back pointer array (w)
PrintSquares(w, i-1, w[i, j]);
}

We are done with part 9. In the next part I will explain the Dynamic Programming problem “Integer Knapsack“. Please use the comments section below for questions, corrections or feedback. Thanks for reading.

More from my site

Tags:, ,

About Author

Mohammed Abualrob

Software Engineer @ Cisco

3 Comments
  1. blah

    Shouldn’t it be?

    int maxd = D[n, 1];
    int maxj = 1;

    //For each column in the last row (n)
    for (int j = 2; j maxd)
    {
    //Update max
    maxd = D[n, j]
    //Save column number
    maxj = j;
    }
    }

    Reply
    • Anonymous

      That’s what I’m thinking

      Reply
  2. Anonymous

    cool

    Reply

Add a Comment

Your email address will not be published. Required fields are marked *