Dynamic Programming Integer Knapsack

Integer Knapsack Problem

Welcome! This is part 10 in a series of articles on Dynamic Programming. You can refer to the first part (introduction) by clicking here. Today we are going to discuss the “Integer Knapsack Problem”. Please recall that our problem today is a little bit different from the “01 Knapsack Problem” in which duplicate items are not allowed. The later one is harder and requires more work so please keep that in mind. Now let us get started.

Problem Definition

We have (n) types of items. Each item (i) has a size (Si) and a value (Vi). Duplicate items are allowed. In other words we can use one or more items of the same type. We need to pack some items in a knapsack of capacity (C) such that we get the maximum value without exceeding the capacity of the knapsack.

Solution

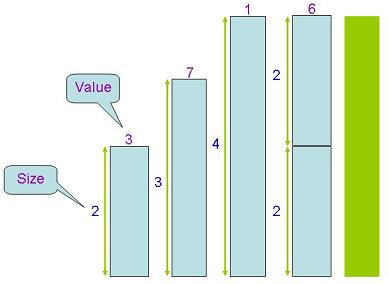
Assume we have a knapsack with a capacity of (4). Assume we have (3) items with the following sizes (2, 3, 4) and values (3, 7, 1). Let us try to fill the knapsack hoping we can achieve maximum value:

1. We can pack just the 1st item (2) and get a value of (3)
2. We can pack just the 2nd item (3) and get a value of (7)
3. We can pack just the 3nd item (4) and get a value of (1)
4. We can pack two copies of the 1st item (2) and get a value of (6)

So the solution to our problem in this case is filling the knapsack with just the second item (3) yielding a maximum value of (7). Here is a schematic diagram to clarify that:

This problem can be solved using a brute force approach as we did in the example above but it is not going to be an efficient solution. On the other hand, this problem can be solved efficiently using Dynamic Programming as it satisfies all the conditions needed to employ a DP technique. So let us do that:

Characterize the structure of an optimal solution

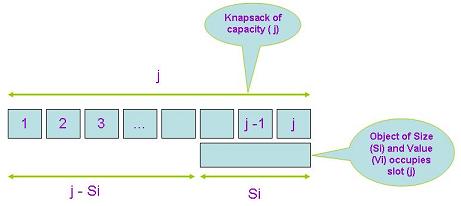
Our goal is to maximize the total value we can possibly get from packing some items in a knapsack of the given capacity. We need to express this value in terms of smaller size problems of the same structure. Think of the knapsack as a container having (j <= C) empty slots each of size (1). Assume we have already filled the knapsack of capacity (j <= C) such that we achieved maximum value. We have two possibilities regarding position (j). It should be either empty or filled with some item. If position (j) is empty then the maximum value we can get is the same as that when filling a knapsack of size (j-1). If position (j) is filled with some item (i) then the maximum value we can get is the value of this item (Vi) plus the maximum value we can get by filling a knapsack of size (j-Si). Since we have multiple items to select from we choose the item that gives us the largest value. Here is a schematic diagram to clarify the second case:

Recursively define the value of an optimal solution

In the first step we characterized the structure of an optimal solution in plain English. Let us now do that formally. Let M(j) be the maximum value we can get from packing some items (subset of the (n) items) into a knapsack of size (j). M(j) can be expressed recursively as:

Let us try to apply the recursive formula above to our example:

As you can see the formula works just fine. The value we get by filling a knapsack of capacity (4) is the same as the value we get by filling a knapsack of capacity (3) because the last slot is kept empty. Note also that sub problems repeat but we have learned from this series that Dynamic Programming saves computed values in a table so that they are used again. In the next step we will compute these values and store them in a table by following a bottom up approach. Once the table M(j) is completely populated we can easily compute the maximum value by simply returning M(C). In order to know which items go to the knapsack we need to use back pointers so let us do that now. Let b(j) point to the previous slot with respect to position (j) that gives us the maximum value. Obviously b(j) is either (j-1) if the jth slot is empty and (j-Si) if the jth slot is occupied by some item (i).

Compute the value of an optimal solution in a bottom up fashion

The following pseudo code populates the values array M(j) and the back pointers array b(j) in a bottom up fashion starting at the initial case when (j=0) then building up all other values. The code is properly commented so take a look:

As you can see we have two nested loops. The first loop runs (n) times and the second loop runs (C) times so the running time of the algorithm is O(n x C) where (n) is the number of items and (C) is the knapsack capacity. The maximum value we can get by filling the knapsack is M(C) but in order to print out the individual items that we need to pack, we need to follow the back pointers saved in b(j). The following section explains how to do that.

Construct an optimal solution from the computed information

In order to print out the individual items that we need to pack in the knapsack we follow the back pointers stored in b(j) starting at (j = C). Just call the following recursive function as:

The pseudo code below prints out the (j) positions at which the packed items start and end positions:

We are done with part 10. In the next part I will explain another Dynamic Programming problem. Please use the comments section below for questions, corrections or feedback. Thanks for reading.