Dynamic Programming: Matrix Chain Multiplication

Matrix Chain Multiplication

Welcome to the third article on Dynamic Programming. You can refer to the first article (introduction) here. Let us get started.

Introduction

Before we formally define our problem let us first refresh our memory about matrix multiplication. In order to multiply two matrices (A) and (B) the number of columns of matrix (A) must match the number of rows of matrix (B). For example if (A) is a (2 x 3) matrix and (B) is a (3 x 2) matrix then the product (C) of the two matrices is going to be a (2 x 2) matrix. Take a look at the following demonstration.

As you can see in the example above the number of scalar multiplications needed to compute the product (C) is (12). Generally speaking if (A) is an (m x k) matrix and (B) is a (k x n) matrix then the product matrix is an (m x n) matrix and the number of scalar multiplications needed is (m x k x n). In our case the number of scalar multiplications is going to be (2 x 3 x 2 = 12). When multiplying two matrices there is always one way to do that however if we have a chain (3 or more) of matrices the problem becomes more interesting. For example if we need to multiply three matrices (D = A x B x C) then there are different ways to do that. Here are the possible ways:

1. Multiply (A) and (B) then multiply the result with (C) to get (D)

2. Multiply (B) and (C) then multiply the result with (A) to get (D)

Both ways yield the same result but the question is which method is more efficient in terms of computational complexity. The one with less scalar multiplications should be more efficient. Does the number of scalar multiplications depend on the order in which we multiply matrices. The answer to this question is YES. Let us take an example and assume:

To calculate the number of scalar multiplications just apply the rule we discussed earlier (m x k x n)

As you can see (D1) is more efficient to compute as it only involves (24) scalar multiplications compared to (36) in the case of (D2). To conclude the number of scalar multiplications involved in computing the product of a chain of matrices depends on how we choose the parenthesis.

Problem definition

We are now ready to define our problem. Given a chain of matrices:

Any matrix in the chain (call it Ai) is a (p(i-1) x pi) matrix which means number of rows = p(i-1) and number of columns = (pi). Note that the (i) and (i-1) here are just indexes to denote the position of the matrix within the chain. For example p(i-1) does NOT mean (p) multiplied by (i-1) so please keep that in mind. Any two matrices in a row (for example A(i-1) and Ai) must satisfy the following condition: the number of columns (p(i-1)) of the first matrix (A(i-1)) must match the number of rows of the second matrix (Ai). We did not define our problem yet due to the long introduction so let us do that now. Formulate an algorithm to parenthesize the matrix multiplication chain so that the total number of scalar multiplication is minimal.

Solution

We can use brute force to get all possible ways to parenthesize the matrix chain then choose the one with minimum number of scalar multiplications. This solution is suicidal because the running time is exponential. If you do not believe me check this out

The general formula to get the number of ways in terms of (n) is as follows. This sequence grows exponentially.

So we are convinced now that brute force is not a good approach. Since we are talking about Dynamic Programming we will demonstrate that DP is in fact a good approach for the matrix chain multiplication problem. Again we will follow the steps discussed in the first Dynamic Programming article.

Characterize the structure of an optimal solution

Ask the question “what are we intending to optimize?” The answer is number of scalar multiplications. In other words we want to minimize the number of scalar multiplications needed to compute the matrix chain product. In next step we will define this number in terms of smaller size sub problems using recursion.

Recursively define the value of an optimal solution

Here is below a schematic diagram for the matrix chain that we have.

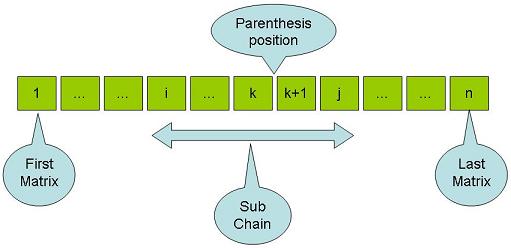
Our matrix chain goes from matrix (1) and ends at matrix (n). A sub problem is another chain that goes from matrix (i) and end at matrix (j) where (i) goes from (1) to (n-1) and (j) goes from (i+1) to (n). Do not be confused about these indexes. We are just saying it is a sub chain that can be anywhere between (1) and (n) that is the whole meaning in plain English.

Let the minimum number of scalar multiplications needed to calculate the sub chain of matrices between (i) and (j) be M[i, j]. As you can see M[i, j] is a two dimensional matrix (or table) where (i) goes from (1) to (n-1) and (j) goes from (i+1) to (n). It is obvious that the minimum number of scalar multiplications need to calculate the whole chain (NOT the sub chain) is M[1, n].

Note that whenever (i == j) the sub chain is a single matrix which means the number of scalar multiplications is ZERO so

if we split the sub chain (i to j) at some position (k) as demonstrated in the schematic diagram above then the number of scalar multiplications needed to compute the sub chain product (i to j) is equal to the number of scalar multiplications needed to compute the sub chain product between (i and k) which is M[i, k] plus the number of scalar multiplications needed to compute the sub chain product between (k + 1 and j) which is M[k + 1, j] plus the number of scalar multiplications needed to compute the product of the two parts of the split (i to k and k + 1 to j) which is P(i-1)P(k)P(j). We can write this formally as

Let me quickly comment on the term P(i-1)P(k)P(j) as it might be confusing how we got that. If you go back to the introduction section we mentioned that if you want to compute the number of scalar multiplications needed to compute the product of two matrices then you multiply (m x k x n) where (m) is the number of rows of the first matrix, (k) is the number of columns of the first matrix and (n) is the number of columns of the second matrix. This is exactly what we did here where P(i-1) is the number of rows of the left side matrix chain split, P(k) is the number of columns of the left matrix chain split and P(j) is the number of columns of the right side matrix chain split (recall that the split was done at some arbitrary position (k)).

We need to find the position (k) between (i) and (j) at which we split the sub chain such that the number of scalar multiplications is minimized. In other words only one (k) value is chosen. We can formulate that as

Let us write the complete recursive formula for the optimal solution

Do not forget that M[i, j] is not only defined recursively in terms of smaller size sub problems but also these sub problems are overlapping otherwise Dynamic Programming wont be of a great value. The sub problems M[i, k] and M[k + 1, j] do overlap. Again the same concept we learned before is applied we only calculate new values but already computed values are just looked up in the table M[i, j].

We are ready now to populate the table M[i, j] and if we substitute (i = 1) and (j = n) we will be able to compute the minimum number of scalar multiplications needed to compute the matrix chain product however that is not what we eventually need. We need to know exactly where to put the parenthesis so that we achieve such an optimal solution. Again this can be taken care of by using back pointers (please refer to the previous articles for more information). Let us use another table called S[i, j] in which we save the values (k) that gives us the minimum number of scalar multiplications needed to compute the sub matrix chain product between (i) and (j). Populating M[i, j] and S[i, j] is done in the next step.

Compute the value of an optimal solution in a bottom up fashion

The following code section demonstrates building M[i, j] in a bottom up fashion. It directly follows the explanation and formula definitions provided earlier so the comments below are more than enough.

Construct an optimal solution from the computed information

The table S[i, j] stores the needed back pointers to construct the final solution (refer to the introduction article for more information about back pointers). For each sub matrix chain product between (i) and (j) there is a stored value (k) in S[i, j]. We use this position to insert a parenthesis. The code below uses a recursive approach to print the overall matrix chain product parenthesized such that minimum number of scalar multiplications is involved. The function receives the back pointers table (S) and two indexes (i) and (j). In order to print the overall solution you need to call the function with (i = 1) and (j = n).

If you take a look at the code that populates the tables. It is not hard to tell that the code runs in polynomial time. We have three nested loop and the worst we can get is O(n^3) but it is actually better than that because the inner loops do not run exactly (n) times. The recursive code used to construct the solution also runs in polynomial time. This proves that Dynamic Programming is a powerful technique if the problem at hand can be solved using DP.

We are done with part 3. In the next part I will explain the third Dynamic Programming problem “Longest Common Subsequence” discussed in “Introduction to Algorithms” by Thomas H. Cormen. Any comments or feedback is appreciated. Thanks for reading.